#문제
11053번: 가장 긴 증가하는 부분 수열
https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
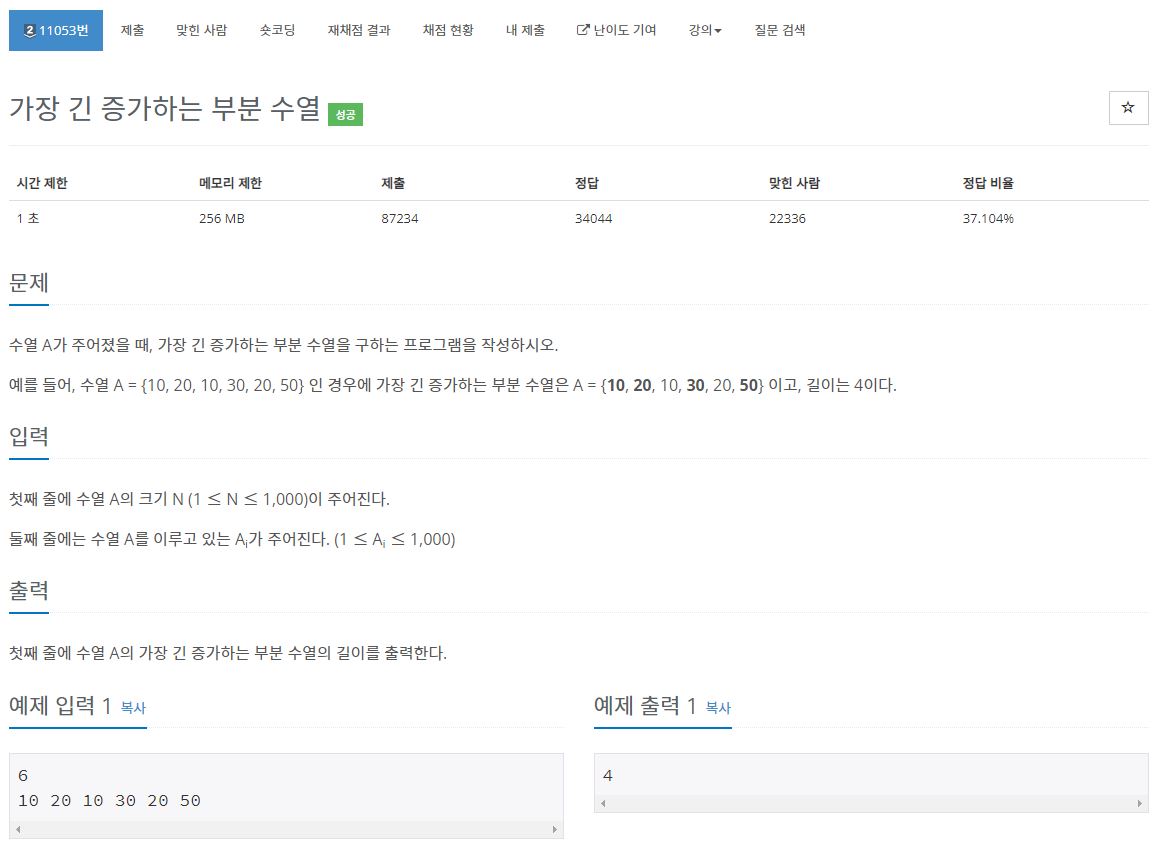
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
#접근방법
수열에서 가장 긴 증가하는 부분 수열을 구하려면 이중 반복문을 돌면서 동적계획법으로 풀면 된다.
#풀이
#include <stdio.h>
int arr[1005];
int dp[1005];
int main(){
int n;
int ans = 0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&arr[i]);
for(int i=1;i<=n;i++){
for(int j=0;j<i;j++){
if(arr[i]>arr[j] && dp[i]<=dp[j]){
dp[i] = dp[j]+1;
if(dp[i]>ans) ans = dp[i];
}
}
}
printf("%d",ans);
return 0;
}
arr배열은 수열이고, dp배열은 동적계획법을 할 때 사용하는 배열이다.
첫번 째 반복문은 1 ~ n까지 수열 전체를 도는 반복문이다.
두번 째 반복문은 0 ~ i-1까지 돌면서 i앞에있는 모든 수열을 도는 반복문이다.
조건문 if(arr[i]>arr[j] && dp[i]<=dp[j])에서 arr[i]>arr[j]의 뜻은
현재 수열에서 i인덱스에 위치하는 값보다 더 작은 값이면 증가하는 부분 수열이므로 dp[i] = dp[j] + 1로 부분 수열의 길이를 갱신해준다.
하지만 이렇게 되면 자신보다 작은 값을 만날 때 마다 최대값이 아닐 때도 갱신이 되므로 dp[i]<=dp[j]의 조건을 넣어서 최대값일 때만 갱신되게 해주었다.
그러면 dp배열의 각각 인덱스에 있는 값들은 최대 부분수열의 길이가 들어있으므로, if(dp[i]>ans) ans = dp[i]라는 조건문으로 dp배열의 최대값을 구해주어서 출력하면 정답이다.
#성능

#정리
반복문을 돌면서 최대값을 갱신할 때, dp[i] = dp[j] + 1과 같이 이미 구한 값을 다시 재사용하는 기술인 동적계획법을 알고 있으면 풀 수 있는 문제였다.
'하루 한 문제' 카테고리의 다른 글
| [백준] 2577번 : 숫자의 개수 [C/C++] (2) | 2021.12.01 |
|---|---|
| [백준] 2562번 : 최댓값 [C/C++] (0) | 2021.11.30 |
| [백준] 2557번 : Hello World [C/C++] (0) | 2021.11.28 |
| [백준] 2475번 : 검증수 [C/C++] (0) | 2021.11.27 |
| [백준] 2439번 : 별 찍기 - 2 [C/C++] (0) | 2021.11.26 |
