#문제
11660번: 구간 합 구하기 5
https://www.acmicpc.net/problem/11660
11660번: 구간 합 구하기 5
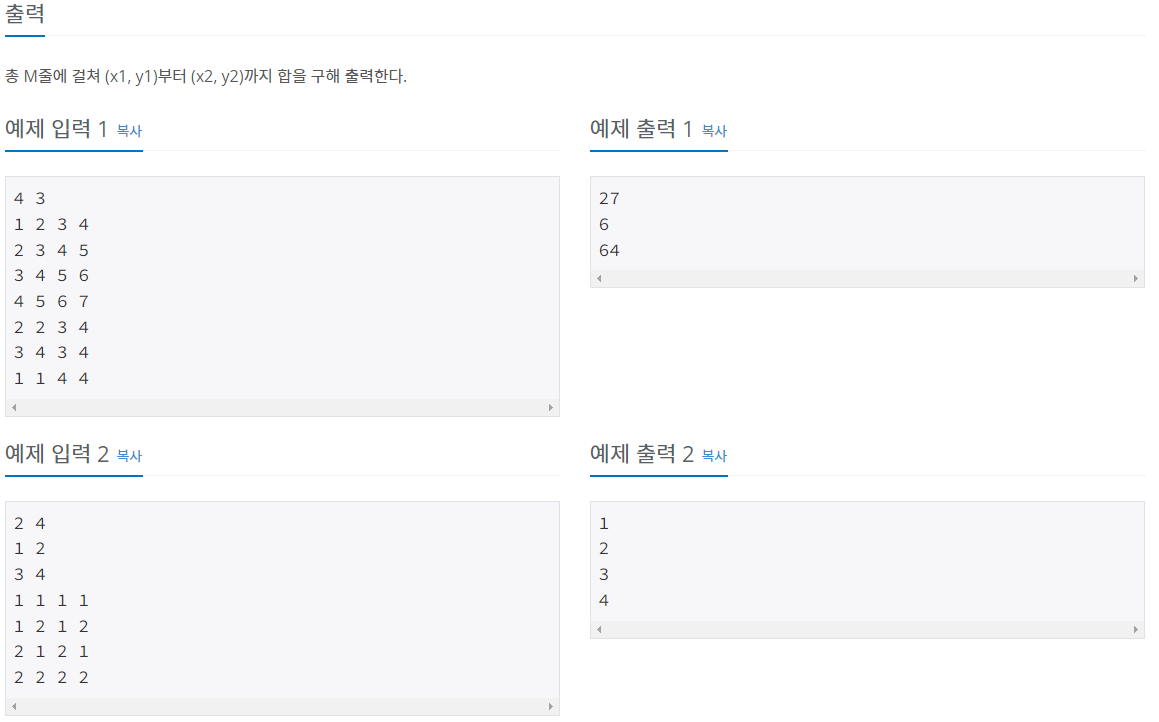
첫째 줄에 표의 크기 N과 합을 구해야 하는 횟수 M이 주어진다. (1 ≤ N ≤ 1024, 1 ≤ M ≤ 100,000) 둘째 줄부터 N개의 줄에는 표에 채워져 있는 수가 1행부터 차례대로 주어진다. 다음 M개의 줄에는 네
www.acmicpc.net

#접근방법
n*n의 배열에 숫자값이 있을 때, (x1,y1), (x2,y2)의 좌표가 들어오면 O(1)번만에 정답을 구해야 시간초과가 걸리지 않는다.
누적합을 시킨 뒤, 적절한 연산을 해주면 쉽게 풀 수 있다.
반응형
#풀이
#include <stdio.h>
int arr[1030][1030];
int main(){
int n,m;
int x1,x2,y1,y2;
scanf("%d %d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
scanf("%d",&arr[i][j]);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
arr[i][j] += arr[i-1][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
arr[i][j] += arr[i][j-1];
for(int i=0;i<m;i++){
scanf("%d %d %d %d",&x1,&y1,&x2,&y2);
printf("%d\n",arr[x2][y2]-arr[x1-1][y2]-arr[x2][y1-1]+arr[x1-1][y1-1]);
}
return 0;
}
먼저 n*n배열을 입력받고, 각각의 arr[i][j]에 (0,0)부터 (i,j)까지의 누적합을 시켜준다.
그리고 (x1,y1), (x2,y2)의 값이 들어오게 되면, 큰 정사각형에 직사각형 2개를 빼준뒤, 중첩되어 빼준 작은 정사각형을 더해주면 (x1,y1) ~ (x2,y2)의 누적값을 구할 수 있다.
이를 식으로 옮기면 arr[x2][y2] - arr[x1-1][y2] - arr[x2][y1-1] + arr[x1-1][y1-1]이 된다.
#성능

#정리
이 문제는 x1 y1 x2 y2의 값이 들어올 때, O(1)의 시간복잡도로 정답을 구할 수 있어야 시간안에 돌아가는 문제였다.
이를 해결하기 위해 배열을 누적 합 시켜서 (x1,y1)에서 (x2,y2)까지의 누적합을 구하기 위한 수식을 생각해낼 수 있으면 쉽게 풀 수 있는 문제였다.
'하루 한 문제' 카테고리의 다른 글
| [백준] 1753번 : 최단경로 [C/C++] (2) | 2021.12.22 |
|---|---|
| [백준] 16953번 : A → B [C/C++] (0) | 2021.12.21 |
| [백준] 9465번 : 스티커 [C/C++] (0) | 2021.12.19 |
| [백준] 5639번 : 이진 검색 트리 [C/C++] (3) | 2021.12.18 |
| [백준] 9498번 : 시험 성적 [C/C++] (0) | 2021.12.18 |
